Con riferimento al diagramma dell’equazione del tempo e in accordo con la seconda legge di Keplero, mi aspettavo un andamento quasi sinusoidale con un massimo e un minimo, invece si hanno due massimi e due minimi nel corso dell’anno. Perché? (Enzo Bartolini, socio A.M.A.)
Per prima cosa occorre ricordare che a base della misura del tempo va posto un movimento continuo ed uniforme a carattere ciclico. Sappiamo che la Terra possiede essenzialmente due movimenti, uno di rotazione attorno al proprio asse, l’altro di rivoluzione attorno al Sole (Prima Legge di Keplero). Dal nostro punto di osservazione (la Terra), i due movimenti reali sono percepiti come moti apparenti. Il primo, come moto di tutta la sfera celeste (sorgere e tramontare degli astri), il secondo, come moto del Sole tra le stelle fisse lungo una traiettoria chiamata eclittica.
Questi due movimenti apparenti permettono di definire rispettivamente i concetti di giorno e di anno (siderale e tropico). I sopraddetti moti apparenti non sono però uniformi e pertanto non sono idonei per la misura del tempo. D’altro canto la vita e le attività dell’uomo sono legate al Sole. Gli astronomi allora, per misurare il tempo, hanno introdotto un Sole fittizio, che percorre l’eclittica con moto uniforme e coincide con il Sole vero all’apogeo e al perigeo. Ma ciò non basta. Occorre tenere conto anche del fatto che il piano dell’eclittica è inclinato rispetto al piano equatoriale di 23° e mezzo circa e che l’intersezione di questi due piani dà luogo ai due cardini chiamati equinozi. Per produrre artificialmente un moto uniforme lungo l’equatore, che rimanga legato al Sole fittizio, occorre introdurre un secondo Sole immaginario che viene chiamato Sole medio coincidente col Sole fittizio ai due equinozi. La differenza tra il tempo solare apparente o vero e il tempo solare medio è una grandezza espressa in minuti chiamata equazione del tempo ( tv – tm = εm ). Il valore di εm è fornito di giorno in giorno da apposite tabelle riportate nelle Effemeridi, oppure può essere ricavato, ma con minore precisione, da un diagramma.
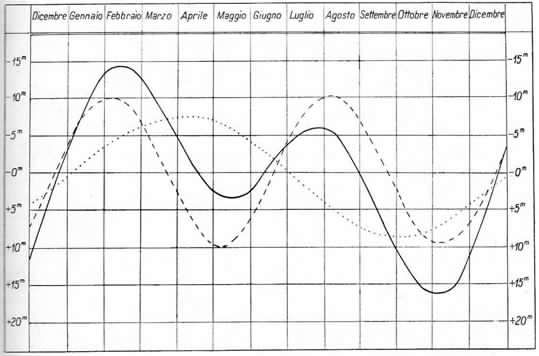
Tale diagramma ha incuriosito il nostro socio, che si chiede perché la curva presenta due massimi e due minimi, invece di un andamento “quasi sinusoidale”, come lui si aspettava. La risposta a questo interrogativo è abbastanza semplice, anche se apparentemente complessa. La curva è data dalla somma algebrica di due componenti, come si vede nella figura: una componente dovuta all’eccentricità dell’orbita della Terra attorno al Sole (Legge di Keplero o delle aree), l’altra dovuta all’inclinazione dell’eclittica sull’equatore. Le due componenti sono curve regolari sinusoidali (con periodo, rispettivamente, di un anno e di sei mesi), espresse da due formule matematiche abbastanza complesse, il cui algoritmo è riportato solo nei testi di Astronomia, che trattano in modo approfondito la misura del tempo. Bisogna tenere presente che l’equazione del tempo diventa nulla quattro volte all’anno: a metà aprile, a metà giugno, all’inizio di settembre e il 24 dicembre, come si vede nel diagramma.
Possiamo concludere dicendo che la curva dell’equazione del tempo nel corso di un anno è una sinusoide irregolare, che presenta due massimi e due minimi (un massimo e un minimo positivi, un massimo e un minimo negativi) e si esprime attraverso una funzione matematica, che fornisce valori approssimati con leggere variazioni da un anno all’altro.
Nell’immagine sotto è riportata la Variazione dell’equazione del tempo nel corso dell’anno (curva a tratto continuo). Il tempo solare apparente, ad una data qualunque, si ottiene aggiungendo algebricamente, al tempo solare medio locale, la correzione indicata dalla curva, in corrispondenza della scala numerica. Le due curve, punteggiata e tratteggiata, rappresentano le due componenti, dovute rispettivamente all’eccentricità dell’orbita terrestre e all’inclinazione dell’eclittica sull’equatore. (Fonte: Il Cielo, G. Cecchini, UTET)
Questo articolo è stato pubblicato sul giornalino Pulsar (numero 39, anno 2013)
